
Loi de Benford
|
La loi de Benford est un étonnant phénomène statistique qui révèle, à l’intérieur de certains ensembles numériques, une régularité numérique très particulière et, au premier abord, contre-intuitive. En fait, cette loi, dite aussi “significant digit-law” (loi des chiffres significatifs), nous démontre que pour certaines données numériques, le premier chiffre des nombres est en majorité le 1, en fait 30% des nombres d’une série donnée commenceront par le chiffre 1. La seconde majorité sera le 2, à 17%, la troisième sera le 3 et ainsi de suite jusqu’à neuf, qui représente moins de 5% des premiers chiffres. C’est-à-dire que pour un ensemble numérique donné, la majorité des nombres débutera par le chiffre 1. Ce qui donne une courbe parfaitement logarithmique allant de 1, plus grande apparition en tête de nombre, au 9, plus petite apparition en tête de nombre. Un ensemble numérique réel peut être, par exemple, la superficie de tous les lacs d’une région donnée, les populations de chaque pays, le taux de mortalité, les statistiques des cas d’infection d’un virus, mon nombre d’abonnés et celui de mes propres abonnés sur Instagram, etc. On y retrouve très souvent une distribution logarithmique des premiers chiffres, une courbe parfaite qui décroît de gauche à droite.
|

|
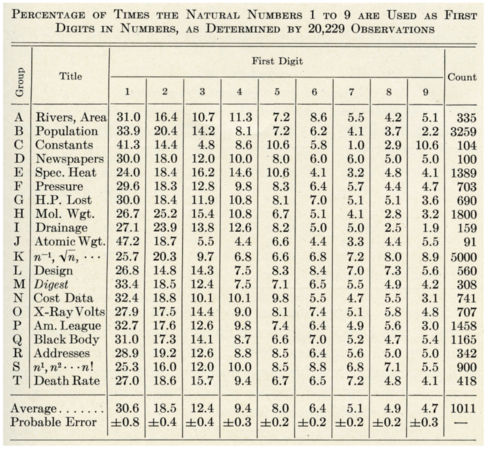
Ce phénomène fut décrit une première fois en 1881 par l’astronome Simon Newcomb qui a remarqué, en consultant un livre sur les logarithmes justement, que les premières pages étaient beaucoup plus abîmées que les dernières, comme si les lecteurs consultaient davantage les premières tables que les dernières. Dès lors, en analysant de plus amples données, il en retira des probabilités significatives, calculées sur des faits réels, démontrant ainsi une loi récurrente, que les chiffres débutant par 1 sont les plus nombreux. Ses écrits furent déterrés 57 ans plus tard, lorsque le physicien Frank Benford s’est également penché sur cet étrange phénomène, publiant un texte intitulé «The Law of Anomalous Numbers», dans lequel il fournit de nouvelles preuves, en analysant 20 000 entrées issues de 20 tables différentes sur diverses informations, comme la chaleur de 1389 composants chimiques, les statistiques de la ligue de baseball américaine, des nombres récoltés sur les premières pages de certains journaux et d’autres données visibles dans le tableau suivant.
|
Simon Newcomb (1835-1909)

|
Frank Benford (1883-1948)

|
|
Parmi ces données, bien que les chiffres ne soient pas parfaitement décroissants, on y voit tout de même une décroissance dans le pourcentage d’apparition des chiffres. Seuls le 1 et le 2 y sont absolument majoritaires, le 3 de justesse et les autres sont en concurrence à certaines rangées. Elles ne suivent donc pas nécessairement une courbe parfaite, mais il y a une tendance évidente à la décroissance entre le 1 et le 9.
|
|
Une question métaphysique
La fréquence de cette loi, apparente en mathématique, mais aussi dans les ensembles de données les plus communs et les plus ordinaires, soulève une question profondément métaphysique sur la nature des chiffres et sur le déterminisme inhérent aux phénomènes physiques. Comme si, malgré nous, nous étions toujours conduits par une proportion naturelle, par un ordre qui s’organise de lui-même et dont nous sommes parfois les acteurs, les opérateurs, sans même nous en rendre compte. Si cette loi, cette voie tracée, s’immisce dans les faits les plus familiers de notre existence, cela signifie-t-il qu’elle agit sur toute action que nous réalisons et sur tout phénomène qui advient? Cette loi est-elle un déterminant actif dans les moindres processus de notre environnement? Ou est-ce que nos moindres mouvements sont naturellement conduits vers cette harmonie et cette proportion universelle? J’imagine que ce sont les deux à la fois; nous sommes à la fois conduits et nous conduisons. C’est-à-dire que lorsque nous agissons selon notre profonde volonté, nous nous synchronisons à l’ordre nécessaire des choses et nous nous plions à l’harmonie sous-jacente de la matière. Apparemment, cette tendance, cette courbe, peut déroger de son chemin lorsque nous allons à l’encontre du cours naturel des choses, lorsque nous modifions les données, ou manipulons les chiffres stratégiquement afin de modifier la réelle apparence des choses. Cette loi est d’ailleurs utilisée en grande partie pour déceler des fraudes ou des falsifications de statistiques, car des données réécrites et modifiées ne respectent pas la loi de Benford. Cette technique est d’ailleurs régulièrement utilisée pour vérifier les résultats d'élection ou encore pour évaluer la légitimité des statistiques de la pandémie du Covid-19. Dès lors, en révélant des contradictions mathématiques, cette loi peut nous aider à discerner le vrai du faux ou, du moins, nous révéler la présence d’un mensonge, d’une dénaturation ou d’une corruption. Mais, bien sûr, l’efficacité et la véracité de cette loi sont remises en question par certains, surtout par des mathématiciens, qui présentent les biais de ce calcul limité et parfois faillible, car bien qu’elle ait pu créer une vaste excitation, elle fut aussi largement critiquée.
Cette découverte nous mène à reconnaître un certain ordre proportionnel dans les choses, à voir le réel comme un immense réseau complexe, régulé par des lois harmonieuses et universelles, toutes choses étant liées entre elles par des mouvements profondément intelligents. La loi de Benford nous permet alors de repenser la nature de nos actions et les véritables causes qui les engendrent et les dirigent. Il ne faut pas pour autant conclure que nous ne sommes que les esclaves d’une mathématique inébranlable, mais plutôt se rappeler que nous faisons partie d’une totalité cohérente et unie par la même nécessité d’être.
BIBLIOGRAPHIE
Arno Berger, Theodore P. Hill. (2015). An Introduction to Benford's Law. Princeton University Press.
Larson, Ben. (2016-12-16). Benford's Law: Fraud Detection by the Numbers. Analytics4all. https://analytics4all.org/2016/11/16/benfords-law-fraud-detection-by-the-numbers/




